Answer:
Perimeter of triangle is 18.
Explanation:
Given:
segment PQ = 1.8
segment PR = 8.2
∠PQR =90°
Since triangle is a right angle triangle with right angle at ∠Q.
Now by using Pythagoras theorem we get;
The square of one side is equal to sum of the square of other two side.
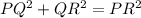
Substituting the given value we get;
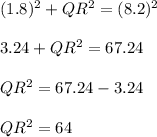
Now taking square root on both side we get;
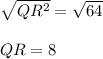
Now we need to find the perimeter of the triangle.
Perimeter of triangle is sum of all three side.
Framing in equation form we get;
Perimeter of triangle = PQ + QR +PR = 1.8 + 8 + 8.2 = 18
Hence Perimeter of triangle is 18.