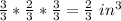Answer:
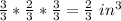
====================================================
Explanation:
The question is missing the attached figure.
The edge of each cube used to build this rectangular prism is 1/3 inch long. Based on the attached figure.
the volume of the prism = length × height × width
length =

height =

width =
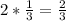
So the volume of the prism =

∴ The equation that shows the volume of the prism, in cubic inches
=