Question

Determine and prove what shape is formed for the given coordinates for ABCD, and then find the

perimeter and area as an exact value.
A (10,-4), B (6,-7), C (3,-3), D (7,0)

Answer 1

Square

Explanation:

Plot points A (10,-4), B (6,-7), C (3,-3), D (7,0) on the coordinate plane.

Find slopes of the sides:

`AB:\ (-7-(-4))/(6-10)=(3)/(4)\\ \\BC:\ (-3-(-7))/(3-6)=-(4)/(3)\\ \\CD:\ (0-(-3))/(7-3)=(3)/(4)\\ \\DA:\ (-4-0)/(10-7)=-(4)/(3)`

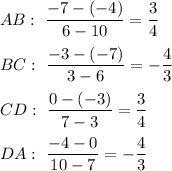
The slopes of opposite sides are the same, so opposite sides are parallel. The slopes of adjacent sides have product of -1, then adjacent sides are perpendicular.

Find the lengths of all sides:

`AB=√((10-6)^2+(-4-(-7))^2)=√(4^2+3^2)=√(16+9)=√(25)=5\ units\\ \\BC=√((6-3)^2+(-7-(-3))^2)=√(3^2+4^2)=√(16+9)=√(25)=5\ units\\ \\CD=√((3-7)^2+(-3-0)^2)=√(4^2+3^2)=√(16+9)=√(25)=5\ units\\ \\AD=√((10-7)^2+(-4-0)^2)=√(3^2+4^2)=√(16+9)=√(25)=5\ units\\ \\`

All four sides are of the same length.

Quadrilateral ABCD is a square (all sides of equal length and perpendicular)