Answer:
Square
Explanation:
Plot points A (10,-4), B (6,-7), C (3,-3), D (7,0) on the coordinate plane.
Find slopes of the sides:
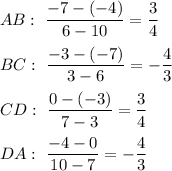
The slopes of opposite sides are the same, so opposite sides are parallel. The slopes of adjacent sides have product of -1, then adjacent sides are perpendicular.
Find the lengths of all sides:
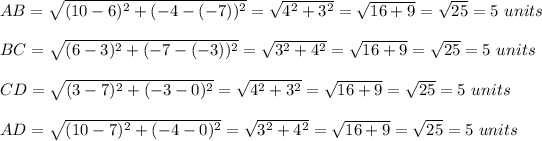
All four sides are of the same length.
Quadrilateral ABCD is a square (all sides of equal length and perpendicular)