Answer:
Step-by-step explanation:
Work is the change in kinetic energy and may be calculated as the product of the force in the direction of the displacement times the displacement.
For a differential displacement, Δx, and a variable force, f(x), the differential work done is:
And the total work done from a point xi to xf is:
Thus, for this problem we have:
- f(x) =
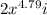
The symbol
 is just indicating that the direction of the force is in the same direction of the displacement.
is just indicating that the direction of the force is in the same direction of the displacement.
Integrating you get:
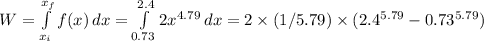
And that is 54.8697 joules (since the units for x are meter and the units for f(x) are newtons).
Rounded to two significant digits: 55 joules.