Question

A certain aircraft can fly 798 miles with the wind in 3 hours and travel the same distance against the wind in 7 hours. What is the speed of the wind?

How do I set up the equations?

Answer 1

76 mph

Explanation:

Let x mph be the speed of the aircraft and y mph be the speed of the wind.

With the wind:

Distance = 798 miles

Time = 3 hours

Speed = x + y mph

Then

`3(x+y)=798\\ \\x+y=266`

Against the wind:

Time = 7 hours

Speed = x - y mph

Then

`7(x-y)=798\\ \\x-y=114`

Add these two equations:

`x+y+x-y=266+114\\ \\2x=380\\ \\x=190\ mph`

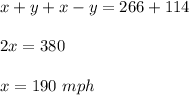
Subtract these two equations:

`(x+y)-(x-y)=266-114\\ \\x+y-x+y=152\\ \\2y=152\\ \\y=76\ mph`

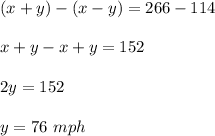
The speed of the aircraft is 190 mph, the speed of the wind is 76 mph