Question

Do you think the shape of the curve on your graph would change if you increased the half-life to 20 seconds? What does this reveal about radioactive decay?

Answer 1

I'm going to give you the answers to the whole project. They are correct.

Step-by-step explanation:

My hypothesis was that every time that they would pour out the pennies the undecayed pennies would decrease in number slowly. According to my data and my graph, my hypothesis was somewhat right and somewhat wrong, the pennies did decrease, but they did so in a fast way. A half-life is Half-life, in radioactivity, the interval of time required for one-half of the atomic nuclei of a radioactive sample to decay, or, equivalently, the time interval required for the number of disintegration per second of radioactive material to decrease by one-half. A radioactive sample emits the most radiation as soon as it is formed or isolated. The reason is that is when the concentration of the radioactive material is the greatest. It begins to decay immediately and as it does, the concentration of radioactive material in the sample gets less. This process can take milliseconds or millions of years depending upon the rate at which the substance breaks down. The reason it's important is that we need to know how long a radioactive material will take to decay to the point that there is so little left that it no longer poses a threat to life. The curve is constant. You will have a large drop at the beginning leaning into a small curve that slowly goes to zero. This is because when the concentration of the radioactive material is the greatest it begins to decay immediately and as it does, the concentration of radioactive material in the sample decreases. No matter the number, the curve stays the same. The curve is still exponential but decreases at a lower rate for a greater half-life; the greater the half-life, the slower radioactive decay is.

Answer 2

The curve is still exponential but decreases at a lower rate for a greater half-life;

The greater the half-life, the slower radioactive decay is.

Step-by-step explanation:

From the context of the actual problem, it looks like you plotted the number of non-decayed atoms against time. Since you are analyzing a radioactive decay in this problem, the number of the atoms remaining for the first-order rate law can be represented by the following equation:

`m_t = m_o e^(-kt)`

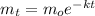
Here k is the rate constant. It is defined in terms of half-life by the following relationship:

`k = \frac{ln(2)}{T_{(1)/(2)}}`

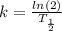
That said, in terms of half-life, our equation becomes:

`m_t = m_o e^(-kt)=m_o e^{-\frac{ln(2)}{T_{(1)/(2)}}t}`

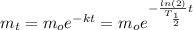
Notice that the greater the half-life is, the less negative the coefficient in front of the time variable in the exponent.

As a result, the decay for a greater half-life would occur at a lower rate. The curve would still be exponential in terms of shape but would decrease at a lower rate.

We may conclude that the greater the half-life, the slower radioactive decay is.