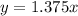Answer:
Yes, "y" varies directly with "x".
The equation is:
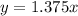
Explanation:
By definition, Direct variation equations have the following form:

Where "k" is the Constant of variation.
If you solve for "k", the equation is:
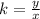
Then, given the table provided in the exercise, you can know if "y" varies directly with "x" by finding the quotient of the correspoding values of "x" and "y":
- Dividing
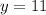 by
by
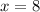 you get:
you get:
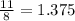
- Divide
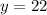 by
by
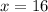 :
:
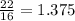
- Dividing
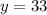 by
by
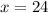 :
:
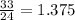
Since the quotient is constant, then "y" varies directly with "x" and the the Constant of variation is:

Therefore, the equation for the Direct variation is: