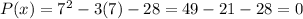Question

Which of the following polynomials has zeros at x = -4 and x = 7?

4x2 = 7x - 11
44²-49
7x² - 4x+28
x²-3x-28

Answer 1

`P(x)=x^2-3x-28`

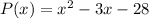
Last option

Explanation:

Roots (Zeros) of Polynomials

A given polynomial P(x) is said to have a root or zero at x=a if P(a)=0.

We must find a polynomial which zeros are x=-4 and x=7. We can test each option, but let's derive the polynomial by multiplying the factors (x+4)(x-7)

`(x+4)(x-7)=x^2-7x+4x-28=x^2-3x-28`

So if our polynomial was

`P(x)=x^2-3x-28`

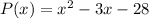
its zeros will be x=-4 and x=7

Testing x=-4

`P(x)=(-4)^2-3(-4)-28=16+12-28=0`

Testing x=7

`P(x)=7^2-3(7)-28=49-21-28=0`