Answer:
See explanation
Explanation:
If
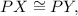 then triangle PXY is isosceles triangle. Angles adjacent to the base XY of an isosceles triangle PXY are congruent, so
then triangle PXY is isosceles triangle. Angles adjacent to the base XY of an isosceles triangle PXY are congruent, so

and
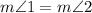
Angles 1 and 3 are supplementary, so
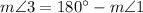
Angles 2 and 4 are supplementary, so
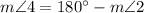
By substitution property,
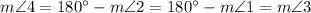
Hence,

Consider triangles APX and BPY. In these triangles:
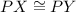 - given;
- given;
 - given;
- given;
 - proven,
- proven,
so
 by ASA postulate.
by ASA postulate.
Congruent triangles have congruent corresponding sides, then

Therefore, triangle APB is isosceles triangle (by definition).