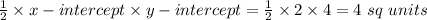Answer:
Area of the bounded region = 4 sq units
Explanation:
The region bounded by y-axis,x-axis and the given line is in the shape of a right-angled triangle which is right-angled at origin.
Hence :
Area of the bounded region = Area of the right-triangle formed
=
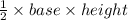
Base length of the Δ = x-intercept of the line
Height of the Δ = y-intercept of the line.
x-intercept is obtained by putting y=0 in the equation y=-2x+4
∴x-intercept = 2
y-intercept is obtained by putting x=0 in the equation y=-2x+4
∴y-intercept = 4
Area of the right-triangle =