Question

An open top box is to be constructed by cutting out squares corners from each end Of a rectangular sheet of copper, folding up the ends and then welding the ends together. Find the dimensions of the box if the original length is 48 inches and width is 36 inches whose base is to have an area of 1260 square inches.

Answer 1

`\displaystyle 48-2(3)=42\ inches`

`\displaystyle 36-2(3)=30\ inches`

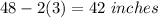
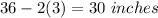
The height of the box is 3 inches

Explanation:

A box has three perpendicular dimensions (a,b,c). Let's assume a and b are the dimensions of the base, and c is the height. The volume of the box is

`\displaystyle V=a\ b\ c`

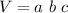
And the area of the base is

`\displaystyle A=a\ b`

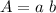
The rectangular sheet of copper has dimensions 48 inches and 36 inches. We are cutting out squares corners from each end.

Set x=side of each square corner. Those corners will be folded up, leaving a base of dimensions (36-2x) and (48-2x). Its area is

`\displaystyle A=(36-2x)(48-2x)`

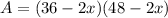
According to the conditions of the question that area must be 1260 square inches, so

`\displaystyle (36-2x)(48-2x)=1260`

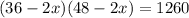
Operating

`\displaystyle 1728-168x+4x^2=1260`

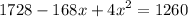
Rearranging

`\displaystyle 4x^2-168x+468=0`

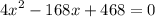
Dividing by 4

`\displaystyle x^2-42x+117=0`

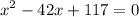
Factoring

`\displaystyle (x-3)(x-39)=0`

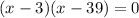
We find two solutions

`\displaystyle x=3\ ,\ x=39`

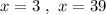
The solution x=39 is unfeasible because it will result in negative dimensions of the base of the box. We keep x=3 as the solution. The dimensions of the base are

`\displaystyle 48-2(3)=42\ inches`

`\displaystyle 36-2(3)=30\ inches`

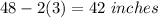
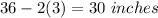
And the height of the box is x=3