Question

At a dance party a group of boys and girls exchange dances as follows: one boy dances with 5 girls, a second boy dances with 6 girls, and so on, the last boy dancing with all the girls. If b represents the number of boys and g represents the number of girls, then find b in terms of g.

Answer 1

b in terms of g is b = g - 4

Solution:

Given that At a dance party a group of boys and girls exchange dances as follows:

Let "b" represents the number of boys

Let "g" represents the number of girls

To find: find b in terms of g

one boy dances with 5 girls, a second boy dances with 6 girls, and so on, the last boy dancing with all the girls.

Set up the following sequence, a one to tone correspondence between the elements of the boy set and the girl set:

Boy number = 1, 2, 3, 4, ....., b

Girl number = 5, 6, 7, ........., b + 4

g = b + 4

b = g - 4

Method 2:

Boy number = 1, 2, 3, 4, ....., b

Girl number = 5, 6, 7, ........., b + 4

Consider the arithmetic sequence 5, 6, 7, ........., b + 4 which is also equivalent to 5,6,7, ...... g

The formula for arithmetic sequence is:

`a_n = a + (n - 1)d`

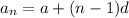
Where
`a_n` is the nth term of sequence

a is the first term of sequence

d is the common difference between terms

Here in the sequence 5, 6, 7, ...... g

`a_n = g\\\\a = 5\\\\d = 6 - 5 = 1`

Hence we get,

g = 5 + (b - 1)1

g = 5 + b - 1

g = b + 4

b = g - 4

Thus b in terms of g is found out