Question

12.Find the point on the x-axis which is equidistant from(2,-5)and(-2,9).

Answer 1

(- 7, 0 )

Explanation:

let the point on the x- axis be (x, 0 )

Then the distance from (x, 0) to (2, - 5) and (- 2, 9) is equal

Use the distance formula to calculate the distances

d = √ (x₂ - x₁ )² + (y₂ - y₁ )²

with (x₁, y₁ ) = (2, - 5) and (x₂, y₂ ) = (x, 0)

d =
`√((x-2)^2+(0+5)^2)`

=
`√((x-2)^2+5^2)` =
`√((x-2)^2+25)`

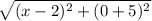
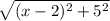Repeat with

(x₁, y₁ ) = (- 2, 9) and (x₂, y₂ ) = (x, 0)

d =
`√((x+2)^2+(0-9)^2\\)`

=
`√((x+2)^2+(-9)^2)` =
`√((x+2)^2+81)`

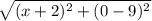
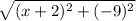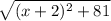
Equating both distances

`√((x-2)^2+25)` =
`√((x+2)^2+81)`

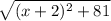
Squaring both sides

(x - 2)² + 25 = (x + 2)² + 81 ← expand parenthesis on both sides

x² - 4x + 4 + 25 = x² + 4x + 4 + 81, that is

x² - 4x + 29 = x² + 4x + 85 ← subtract x² + 4x from both sides

- 8x + 29 = 85 ( subtract 29 from both sides )

- 8x = 56 ( divide both sides by - 8 )

x = - 7

Thus the point on the x- axis is (- 7, 0 )