Question

Tom simplified an expression in three steps, as shown: x to the power of negative 2 multiplied by y to the power of 4, over y multiplied by x to the power of 4 multiplied by x to the power of 4 multiplied by y to the power of negative 2, the whole to the power of 4 equal to x to the power of 2 multiplied by y to the power of 8, over y to the power of 4 multiplied by x to the power of 8 multiplied by x to the power of 8 multiplied by y to the power of 2 equal to x to the power of 2 multiplied by y to the power of 8, over y to the power of 6 multiplied by x to the power of 16.

Answer 1

Step 1 is correct

Answer 2

Answer: Step 1, all the exponents are increased by 4.

Explanation:

The missing question is: "Which is the first incorrect step and why?

Step 1, all the exponents are increased by 4.

Step 2, the exponents of the same base are added during multiplication.

Step 3, the exponents of the same base are subtracted during division.

Step 3, all the exponents are added during division."

The steps are attached.

To solve this exercise it is necessary to remember the following properties:

1. The Product of powers property states that:

`(a^m)(a^n)=a^((m+n))`

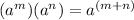
2. The Quotient of powers property states that:

`(a^m)/(a^n)=a^((m-n))`

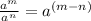
3. The Power of a power property states that:

`(a^m)^n=a^((mn))`

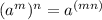
4. By the Negative exponent rule:

`a^(-n)=(1)/(a^n)`

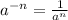
Then, given the following expression:

`((x^(-2)y^4)/(yx^4*x^4y^(-2)))^4`

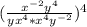
The first step you can apply in order to simplify it is to use the Power of a power property and multiply all the exponents inside the parentheses by the exponent 4 that is outside of the parentheses:

`(x^(-8)y^(16))/(y^4x^(16)*x^(16)y^(-8))`

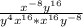
Based on this, you can identify that Tom made a mistake in Step 1, because he did not apply the Power of a powet property but increased all the exponents inside the parentheses by 4.