To solve this problem it is necessary to apply the concepts related to the Power defined from the Stefan-Boltzmann equations.
The power can be determined as:
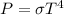
Making the relationship for two states we have to
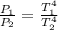
Since the final power is 8 times the initial power then

Substituting,
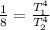
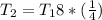
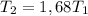
The temperature increase would then be subject to
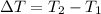
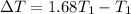
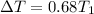
The correct option is D, about 68%