Answer:
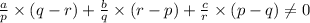 is proved for the sum of pth, qth and rth terms of an arithmetic progression are a, b,and c respectively.
is proved for the sum of pth, qth and rth terms of an arithmetic progression are a, b,and c respectively.
Explanation:
Given that the sum of pth, qth and rth terms of an arithmetic progression are a, b and c respectively.
First term of given arithmetic progression is A
and common difference is D
ie.,
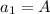 and common difference=D
and common difference=D
The nth term can be written as
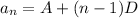
pth term of given arithmetic progression is a
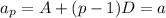
qth term of given arithmetic progression is b
 and
and
rth term of given arithmetic progression is c

We have to prove that

Now to prove LHS=RHS
Now take LHS
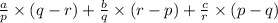
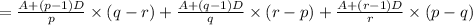
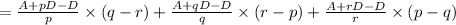
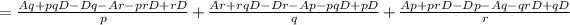
![=([Aq+pqD-Dq-Ar-prD+rD]* qr+[Ar+rqD-Dr-Ap-pqD+pD]* pr+[Ap+prD-Dp-Aq-qrD+qD]* pq)/(pqr)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ek7shr0ra8n1eh8xu21ku8ukuaac3dunsk.png)
![=(Arq^(2)+pq^(2) rD-Dq^(2) r-Aqr^(2)-pqr^(2) D+qr^(2) D+Apr^(2)+pr^(2) qD-pDr^(2) -Ap^(2)r-p^(2) rqD+p^(2) rD+Ap^(2) q+p^(2) qrD-Dp^(2) q-Aq^(2) p-q^(2) prD+q^(2)pD)/(pqr)]()

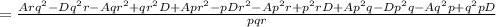
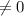
ie.,
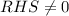
Therefore

ie.,
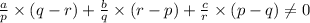
Hence proved