To solve this problem it is necessary to apply the concepts related to the elastic potential energy from the simple harmonic movement.
Said mechanical energy can be expressed as

Where,
k = Spring Constant
A = Cross-sectional Area
From the angular movement we can relate the angular velocity as a function of the spring constant and the mass in order to find this variable:
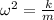
 for f equal to the frequency.
for f equal to the frequency.
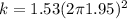
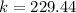
Finally the energy released would be
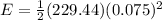
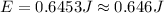
Therefore the correct answer is B.