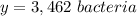Answer:
Explanation:
In this problem we have a exponential function of the form
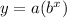
where
x is the time in hours
y is the numbers of bacteria
a is the initial value
b is the base
r is the rate of growth
b=(1+r)
we have that
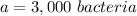
For x=8, y=3,300
substitute in the exponential function
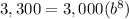
solve for b
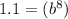
![b=\sqrt[8]{1.1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pqcxb6ygrvvd9hu4uoc5gl5dsfzzmxobuo.png)
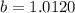
Find the value of r
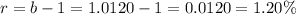
The equation is equal to
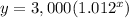
For x=12 hours
substitute the value of x in the equation