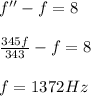Question

A bat flies toward a wall, emitting a steady sound of frequency f in its own reference frame. The bat hears its own sound plus the sound reflected by the wall, which together produce a beat frequency of 8.00 Hz. If the bat is flying at 1.00 m/s, what is the frequency f? (You may take the speed of sound in air to be 344.0 m/s.)

Answer 1

1372 Hz

Step-by-step explanation:

`f` = actual frequency emitted by bat

Consider the wall as the listener and bat as the source of sound

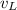`v_(L)` = speed of listener = 0 m/s

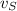`v_(S)` = speed of source =
`v`

`V` = Speed of sound = 344 m/s

`f'` = frequency observed by wall

Since source is moving towards the listener, using Doppler's law

`f' = ((V - V_(L))f)/(V - V_(s)) \\f' = ((V - 0)f)/(V - v)\\f' = (344f)/(344 - v)`

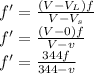
After sound gets reflected, Consider the wall as the source and bat as the listener.

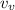`v_(v)` = speed of listener(bat) = v

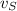`v_(S)` = speed of source(wall) = 0

`V` = Speed of sound = 344 m/s

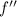`f''` = frequency of the reflected sound heard by bat

Since listener(bat) is moving towards the source(wall), using Doppler's law

`f'' = ((V + V_(L))f')/(V - V_(s)) \\f'' = ((V + v)f')/(V - 0)\\f'' = ((344 + v)f')/(344)\\ f'' = ((344 + v))/(344)(344f)/(344 - v)\\ f'' = ((344 + v)f)/((344 - v))\\ f'' = ((344 + 1)f)/((344 - 1))\\ f'' = (345f)/(343)`

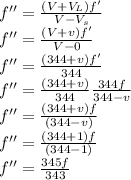
It is given that

`f'' - f = 8 \\\\(345f)/(343) -f = 8\\\\f = 1372 Hz`