Question

The Best Company produces two commercial products : blenders and mixers. Both products require a two step production process involving delivery of parts (JIT process) and assembly. It takes 1 hour to deliver parts for each blender and 2 hours for each mixer. Final assembly of mixers and blenders require 3 and 2 hours, respectively. The production capability is such that only 24 hours of delivery time and 30 hours of assembly time are available. Each blender produced nets the firm $7 and each mixer $6.

a) How many of each should be produced to maximize profit? Partial production of each product is allowed.
b) What is the $ amount of this profit?

Answer 1

Maximum profit is $87 when 3 blenders and 11 mixers are produced.

Explanation:

let blender is represented by
`x_(1)` and and mixer by
`x_(2)`.

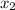total time to deliver parts = 24 hrs

total time to assemble = 30 hrs

time taken by each blender to deliver parts = 1 hr

time taken by each mixer to deliver parts = 2 hr

time taken by blenders in final assembling= 2 hr

time taken by mixers in final assembling = 3 hr

Each blender produced nets the firm= $7

Each mixer produced nets the firm= $6

Using this all data linear system of equation will be:

`x_(1) + 2x_(2) =24  ----- (1)\\2x_(1) + 2x_(2) = 30 ----- (2)\\`

profit function:

`z= 7x_(1) +6x_(2) --- (3)`

`from (1)\\x_(1) = 0 \implies x_(2)= 12\\x_(2)= 0 \implies x_(1)= 24\\`

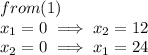
Coordinate points obtained from (1) are (0,12) and (24,0)

`from (2)\\x_(1)=0 \implies x_(2)=10\\x_(2)=0 \implies x_(1)=15\\`

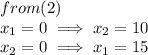
Coordinate points obtained from (2) are (0,10) and (15,0)

plotting these on graph

points lying in feasible region are:

A(0,0)

B(0,10)

C(3,11)

D(12,0)

substituting these points in (3) to find the maximum profit:

for A (0,0)

z = 0

for B (0,10)

z = 60

for C (3,11)

z = 87

for D (12,0)

z=84

So maximum profit is $87 when 3 blenders and 11 mixers are produced.