Question

A simple random sample of 100 batteries is selected from a process that produces batteries with a mean lifetime of 32 hours and a standard deviation of 3 hours. Thus the standard deviation of the sampling distribution is equal to 0.3.

If the sample size is changed to 400, what is the new standard deviation of the sampling distribution?a. It is one‐fourth as large as when n = 100.b. It is one‐half as large as when n = 100.c. It is twice as large as when n = 100.d. It is four times as large as when n = 100.e. The value of σ does not change.

Answer 1

.b. It is one‐half as large as when n = 100.

Explanation:

Given that a simple random sample of 100 batteries is selected from a process that produces batteries with a mean lifetime of 32 hours and a standard deviation of 3 hours.

i.e. s = 0.3

we obtain se of sample by dividing std devitation by the square root of sample size

i.e. s=
`(3)/(√(n) )`

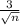
when n =100 this = 0.3 and

when n =400 this equals 0.15

We find that when sample size is four times as large as original, std deviation becomes 1/2 of the original

Correction option is

.b. It is one‐half as large as when n = 100.