Question

A rock thrown vertically upward from the surface of the moon at a velocity of 36​m/sec reaches a height of s = 36t - 0.8 t^2 meters in t sec.

a. Find the​ rock's velocity and acceleration at time t.
b. How long does it take the rock to reach its highest​ point?
c. How high does the rock​ go?
d. How long does it take the rock to reach half its maximum​ height?
e. How long is the rock​ a loft?

Answer 1

a. The rock's velocity is
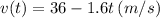`v(t)=36-1.6t \:{(m/s)}` and the acceleration is
`a(t)=-1.6  \:{(m/s^2)}`

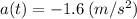
b. It takes 22.5 seconds to reach the highest point.

c. The rock goes up to 405 m.

d. It reach half its maximum height when time is 6.59 s or 38.41 s.

e. The rock is aloft for 45 seconds.

Explanation:

• Velocity is defined as the rate of change of position or the rate of displacement.
  `v(t)=(ds)/(dt)`
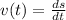
• Acceleration is defined as the rate of change of velocity.
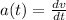
  `a(t)=(dv)/(dt)`

a.

The rock's velocity is the derivative of the height function
`s(t) = 36t - 0.8 t^2`

`v(t)=(d)/(dt)(36t - 0.8 t^2) \\\\\mathrm{Apply\:the\:Sum/Difference\:Rule}:\quad \left(f\pm g\right)'=f\:'\pm g'\\\\v(t)=(d)/(dt)\left(36t\right)-(d)/(dt)\left(0.8t^2\right)\\\\v(t)=36-1.6t`

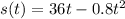
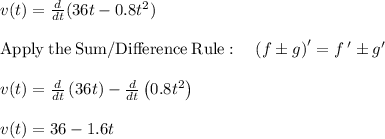
The rock's acceleration is the derivative of the velocity function
`v(t)=36-1.6t`

`a(t)=(d)/(dt)(36-1.6t)\\\\a(t)=-1.6`

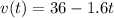
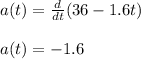
b. The rock will reach its highest point when the velocity becomes zero.

`v(t)=36-1.6t=0\\36\cdot \:10-1.6t\cdot \:10=0\cdot \:10\\360-16t=0\\360-16t-360=0-360\\-16t=-360\\t=(45)/(2)=22.5`

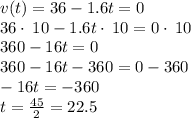
It takes 22.5 seconds to reach the highest point.

c. The rock reach its highest point when t = 22.5 s

Thus

`s(22.5) = 36(22.5) - 0.8 (22.5)^2\\s(22.5) =405`

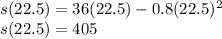
So the rock goes up to 405 m.

d. The maximum height is 405 m. So the half of its maximum height =
`(405)/(2) =202.5 \:m`

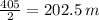
To find the time it reach half its maximum height, we need to solve

`36t - 0.8 t^2=202.5\\36t\cdot \:10-0.8t^2\cdot \:10=202.5\cdot \:10\\360t-8t^2=2025\\360t-8t^2-2025=2025-2025\\-8t^2+360t-2025=0`

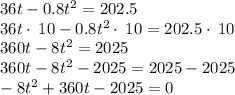
For a quadratic equation of the form
`ax^2+bx+c=0` the solutions are

`x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

`\mathrm{For\:}\quad a=-8,\:b=360,\:c=-2025:\\\\t=(-360+√(360^2-4\left(-8\right)\left(-2025\right)))/(2\left(-8\right))=(45\left(2-√(2)\right))/(4)\approx 6.59\\\\t=(-360-√(360^2-4\left(-8\right)\left(-2025\right)))/(2\left(-8\right))=(45\left(2+√(2)\right))/(4)\approx 38.41`

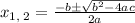
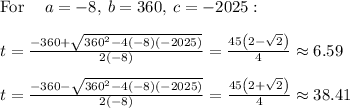
It reach half its maximum height when time is 6.59 s or 38.41 s.

e. It is aloft until s(t) = 0 again

`36t - 0.8 t^2=0\\\\\mathrm{Factor\:}36t-0.8t^2\rightarrow -t\left(0.8t-36\right)\\\\\mathrm{The\:solutions\:to\:the\:quadratic\:equation\:are:}\\\\t=0,\:t=45`

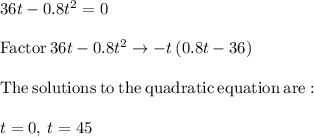
The rock is aloft for 45 seconds.