Answer:
Step-by-step explanation:
a )
When they are at infinite separation , energy of the system is zero
When they are at d separation
potential energy = - G m₁m₂ / d
So there is reduction in potential energy which will increase their kinetic energy by the same amount so that total energy becomes zero again .
Let their velocity becomes v₁ and v₂ respectively
according to c
law of conservation of momentum
m₁v₁ = m₂v₂ ( in magnitude )
Their total kinetic energy
= 1/2 m₁v₁² + 1/2 m₂v₂² = G m₁m₂ / d
= 1/2 m₁v₁² + 1/2 m₂(m₁v₁ / m₂)² = G m₁m₂ / d
= 1/2 m₁v₁² + 1/2 m₁²v₁² / m₂ = G m₁m₂ / d
1/2 m₁v₁²( 1 + m₁ / m₂ ) = G m₁m₂ / d
v₁ =
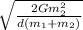
Similarly
v₂ =

Relative velocity = v₁ +v₂
=
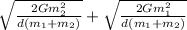
Putting the values in the expression of v₁
we get
v₁ = 7.9 x 10⁷ m / s
v₂ = 1.09 x 10⁷
Kinetic energy of m₁
= .5 x 2.6 x 10²⁴ x (7.9 x 10⁷)²
= 81.13 x 10³⁸ J