Question

The concept of critical density is just like the idea of escape velocity for a projectile launched from the earth. An object launched with a velocity less than the escape velocity will fall back to the earth, and an object launched with one greater than the escape velocity can escape the earth's gravitational field. Find an expression for vesc, the escape velocity of a projectile launched from the earth's surface. Express your answer in terms of the universal gravitational constant G, the mass of the earth Me, and the radius of the earth Re.

Answer 1

v = √ 2 G M/
`R_(e)`

Step-by-step explanation:

To find the escape velocity we can use the concept of mechanical energy, where the initial point is the surface of the earth and the end point is at the maximum distance from the projectile to the Earth.

Initial

Em₀ = K + U₀

Final

`Em_(f)` =
`U_(f)`

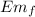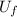
The kinetic energy is k = ½ m v²

The gravitational potential energy is U = - G m M / r

r is the distance measured from the center of the Earth

How energy is conserved

Em₀ =
`Em_(f)`

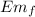
½ mv² - GmM /
`R_(e)` = -GmM / r

v² = 2 G M (1 /
`R_(e)` – 1 / r)

v = √ 2GM (1 /
`R_(e)` – 1 / r)

The escape velocity is that necessary to take the rocket to an infinite distance (r = ∞), whereby 1 /∞ = 0

v = √ 2GM /
`R_(e)`