Answer:
A =
 , a = 9.4 , and b = 7.5 (which coincides with option C among the listed possible answers)
, a = 9.4 , and b = 7.5 (which coincides with option C among the listed possible answers)
Explanation:
First, we can find the length of side b through the law if sines:
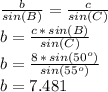
That we can round to 7.5
Now we can find angle A using the property that the addition of all angles in a triangle must equal
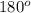 :
:
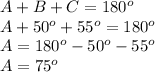
And finally, we can find side "a" by using again the law of sines:
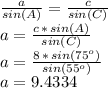
which can be rounded to a = 9.4