Question

You have a triangle that has an altitude 5 inches longer than the base.If the area of your triangle is 63 square inches, what are the dimensions of the base and altitude?

Answer 1

Base of triangle is 9 inches and altitude of triangle is 14 inches.

Explanation:

Given:

Area of Triangle = 63 sq. in.

Let base of the triangle be 'b'.

Let altitude of triangle be 'a'.

Now according to question;

altitude is 5 inches longer than the base.

hence equation can be framed as;

`a=b+5`

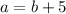
Now we know that Area of triangle is half times base and altitude.

Hence we get;

`(1)/(2) * b * a =\textrm{Area of Triangle}`

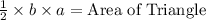
Substituting the values we get;

`(1)/(2) * b * (b+5) =63\\\\b(b+5)=63*2\\\\b^2+5b=126\\\\b^2+5b-126=0`

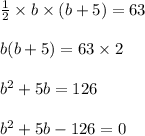
Now finding the roots for given equation we get;

`b^2+14b-9b-126=0\\\\b(b+14)-9(b+14)=0\\\\(b+14)(b-9)=0`

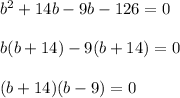
Hence there are 2 values of b
`b-9 = 0\\b=9\\\\b+14=0\\b=-14`

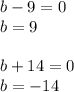
Since base of triangle cannot be negative hence we can say
`b=9\ inches`

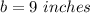
So Base of triangle = 9 inches.

Altitude = 5 + base = 5 + 9 = 14 in.

Hence Base of triangle is 9 inches and altitude of triangle is 14 inches.