Question

A projectile of mass m is fired straight upward from the surface of an airless planet of radius R and mass M with an initial speed equal to the escape speed vesc (meaning the projectile will just barely escape the planet's gravity -- it will asymptotically approach infinite distance and zero speed.) What is the correct expression for the projectile's kinetic energy when it is a distance 9R from the planet's center (8R from the surface). Ignore the gravity of the Sun and other astronomical bodies. KE (at r = 9R) is:a. GMm/9Rb. GMm/8Rc. 1/2mvesc^2d. -GMm/8Re. None of these

Answer 1

K = G Mm / 9R

Step-by-step explanation:

Expression for escape velocity V_e =
`\sqrt{(2GM)/(R) }`

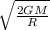
Kinetic energy at the surface = 1/2 m V_e ²

= 1/2 x m x 2GM/R

GMm/R

Potential energy at the surface

= - GMm/R

Total energy = 0

At height 9R ( 8R from the surface )

potential energy

= - G Mm / 9R

Kinetic energy = K

Total energy will be zero according to law of conservation of mechanical energy

so

K - G Mm / 9R = 0

K = G Mm / 9R