Answer:
Correct: Third option μx = 9 and σx = 2.51
Explanation:
Binomial Distribution
Being p the probability of success of an individual event, q the probability of failure (q=1-p) and n the number of independent trials of that event, the expected value or mean of the distribution is

And the variance is
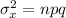
The standard deviation is
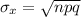
The given binomial distribution has the following parameters
n = 30, p = 0.3, q = 1 - 0.3 = 0.7. The mean is
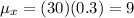
The standard deviation is
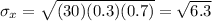
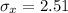
The third option is the correct one