The force required is equal to 148.33 N.
Why?
To answer your question, I'll assume that the value of 0.35 is referring to the coefficient of kinetic friction. So, we can solve the problem using the following equations:
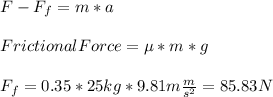
Now, substituting, we have:

Hence, we have that the force required to accelerate the box at a rate of 2.5 m/s2 is 148.33N.
Have a nice day!