Answer:
F = 7476 N
Explanation:
given,
diameter of hemispherical plate = 6 ft
height of submergence = 1 ft
the weight density of water = 62.5 lb/ft³
Assuming that hemispherical plate is residing on x and y axis.
bottom of plate is on x-axis and left side of the plate touches y-axis
now, plate is defined by the upper half of the circle
(x - 3)² + (y-0)² = 3²
y² = 9 - (x - 3)²
y = √(9 - (x - 3)²)
hydro static pressure on one side of plate.
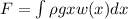

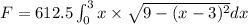
on solving the above equation
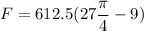
F = 7476 N