Question

A 20 gram charged ball hangs vertically from a thin, massless string. At time t = 0, an electric field whose magnitude is 6.40 × 105N/C is turned on; this field points horizontally to the left. The ball is observed to swing upwards to the right, and when it finally comes to rest, the tension in the string is double what it was in the absence of the field. Find the charge on the ball, and the angle the string makes with the vertical when the field is turned on and the charged ball is at rest.

Answer 1

θ = 60° , q = 5.3044 10⁻⁷ C

Step-by-step explanation:

We must solve this problem with Newton's second law of equilibrium applied to each axis.

Y Axis

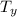`T_(y)` - W = 0

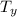`T_(y)` = W

X axis

-Tₓ +
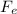`F_(e)` = 0

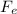`F_(e)` = Tₓ

Electric force is

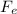`F_(e)` = q E

Let's use trigonometry to find the components, the angle is average with respect to the vertical

sin θ = Tₓ / T

cos θ =
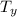`T_(y)` / T

Tₓ = T sin θ

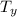`T_(y)` = T cos θ

We replace

T cos θ = mg

T sin θ = q E

Before turning on the electric field the system is in a vertical balance

To- W = 0

To = W = mg

In the exercise they indicate that when the field is connected the voltage of twice the initial voltage

T = 2 To

We replace

2To cos θ = mg

2To sin θ = q E

2 mg cos θ = mg

cos θ = ½

θ = cos⁻¹ (1/2)

θ = 60°

Now let's use the other equation

2 mg sin θ = q E

q = 2 m g sin θ / E

We reduce the magnitudes to the SI system

m = 20 g (1 kg / 10³ g) = 20 10⁻³ kg

Let's calculate

q = 2 20 10⁻³ 9.8 sin 60 /6.40 10⁵

q = 5.3044 10⁻⁷ C