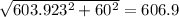Answer:
The speed of the aircraft relative to the ground is 606.9
Step-by-step explanation:
x-y coordinate system:
x is Positive due East direction. Similarly y is Positive due North Direction.
Now let us Decompose each vector into x-y
500 km/h due east = (500, 0)
120 km/h at 30 degree north of east
=
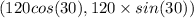
=
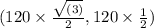
=
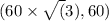
Adding the vectors.
=
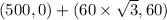
=

=
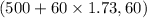
=
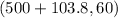
= (603.8, 60)
Returning back to polar form
Magnitude =