Question

Two methanol-water mixtures are contained in separate tanks. The first mixture contains 40.0 wt% methanol and the second contains 70.0 wt% methanol. If 200 kg of the first mixture is combined with 150 kg of the second, what are the mass and composition of the product? How many independent material balances can be written?

Answer 1

`M_(per)= 52.86`

`W_(per)=47.14`

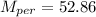
Step-by-step explanation:

First mixture:

40 wt% methanol - 60 wt% water 200 kg

`m_(met1)=200 kg * 0.4= 80 kg`

`m_(wat1)=200 kg * 0.6= 120 kg`

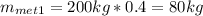
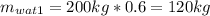
Second mixture:

70 wt% methanol - 30 wt% water 150 kg

`m_(met2)=150 kg * 0.7= 105 kg`

`m_(wat2)=150 kg * 0.3= 45 kg`

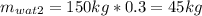
Final mixture:

`m_{metF=80 kg + 105 kg= 185 kg`

`m_(watF)=120 kg + 45 = 165 kg`

`M_(per)=(185 kg)/(185 kg + 165 kg)*100= 52.86`

`W_(per)=(165 kg)/(185 kg + 165 kg)*100=47.14`

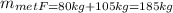
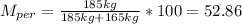
If, the compositions are constant, the only variables are the mass of each mixture used in the final one, so there can be only one independent balance.