Question

A Hall-effect probe to measure magnetic field strengths needs to be calibrated in a known magnetic field. Although it is not easy to do, magnetic fields can be precisely measured by measuring the cyclotron frequency of protons. A testing laboratory adjusts a magnetic field until the proton's cyclotron frequency is 9.70 MHz . At this field strength, the Hall voltage on the probe is 0.549 mV when the current through the probe is 0.146 mA . Later, when an unknown magnetic field is measured, the Hall voltage at the same current is 1.735 mV .

A) What is the strength of this magnetic field?

Answer 1

The value of the magnetic field is 2.01 T when Hall voltage is 1.735 mV

Step-by-step explanation:

The frequency of the cyclotron can help us find the magnitude of the magnetic field, thus then we can compare the effect of increasing Hall voltage on the probe.

Magnetic field magnitude at initial Hall voltage.

The cyclotron frequency can be written in terms of the magnetic field magnitude as follows

`f = \cfrac{qB}{2\pi m}`

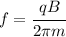
Solving for the magnetic field.

`B = \cfrac{2\pi mf}q`

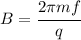
Thus we can replace the given information but in Standard units, also remembering that the mass of a proton is
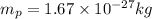`m_p=1.67 * 10^(-27) kg` and its charge is
`q_p=1.6 * 10^(-19) C`.

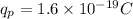So we get

`B = \cfrac{2\pi * 1.67 * 10^(-27) kg * 9.7 * 10^6 Hz}{1.6 * 10^(-19)C}`

`B =0.636 T`

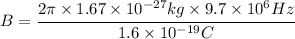
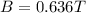
We have found the initial magnetic field magnitude of 0.636 T

Magnetic field magnitude at increased Hall voltage.

The relation given by Hall voltage with the magnetic field is:

`V_H =\cfrac{R_HI}t B`

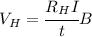
Thus if we keep the same current we can write for both cases:

`V_(H1) =\cfrac{R_HI}t B_1\\V_(H2) =\cfrac{R_HI}t B_2`

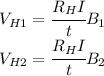
Thus we can divide the equations by each other to get

`\cfrac{V_(H1) }{V_(H2)}=\cfrac{\cfrac{R_HI}t B_1}{\cfrac{R_HI}t B_2}`

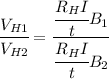
Simplifying

`\cfrac{V_(H1) }{V_(H2)}=\cfrac{ B_1}{ B_2}`

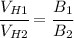
And we can solve for
`B_2`

`B_2 =B_1 \cfrac{V_(H2)}{V_(H1)}`

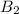
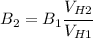
Replacing the given information we get

`B_2= 0.636 T * \left(\cfrac{1.735 mV}{0.549 mV} \right)`

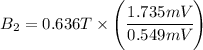
We get

`\boxed{B=2.01\, T}`

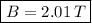
Thus when the Hall voltage is 1.735 mV the magnetic field magnitude is 2.01 T