Answer:
x =23.9 (which matches the last option in the list of possible answers)
Explanation:
Notice that we can use ratios among sides of similar triangles to solve this problem. Notice the two triangles in question. The small triangle is that with sides (x-1) and 20, while the larger triangle is that of larger sides built by the addition of (x-1) + 8 , and by 20 + 7
So we can relate similar sides with their ratios, and say that side (x-1)+8 is to side (x-1) the same as side (20 +7) is to side 20. Such put in math terms becomes the following proportion:
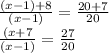
we can now solve for the unknown "x" in the rational equation above, by cross multiplication:
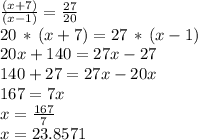
which we can round to 23.9 to match the last option in the list of possible answers.