Question

Determine what shape is formed for the given coordinates for ABCD, and then find the perimeter and area as an exact value and rounded to the nearest tenth.

(NO ABSURD ANSWERS PLEASE !)

Answer 1

The answer to your question is below

Explanation:

The shape is an irregular quadrilateral shape.

Perimeter

1.- Find the length of the four sides

dAB =
`\sqrt{(-5 + 25)^(2) + (-32 + 11)^(2)  }`

=
`\sqrt{20^(2) + 21^(2) }`

=
`√(841)`

= 29 u

dAD =
`\sqrt{(-4 + 25)^(2) + (9 + 11)^(2) }`

=
`\sqrt{21^(2) + 20^(2) }`

=
`√(441 + 400)`

=
`√(841)`

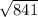
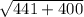
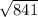
= 29 units

dBC =
`\sqrt{(37 + 5)^(2) + (8 + 32)^(2) }`

=
`\sqrt{42^(2) + 40^(2) }`

=
`√(1764 + 1600)`

=
`√(3364)`

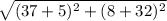
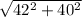
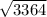
= 58 units

dCD =
`\sqrt{(-4 - 37)^(2) + (9 -8)^(2) }`

=
`\sqrt{-41^(2) + 1x^(2) }`

=
`√(1681 + 1)`

=
`√(1682)`

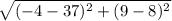
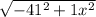
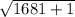
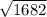
= 41.01 units

Perimeter = 29 + 29 + 58 + 41.01 = 157.01 ≈ 157 units

Area

To find the area divide the figure in a square and a triangle

Area of the square = 29 x 29 = 841 units²

Area of the triangle = (base x height) / 2

base = 58 - 29 = 29

height = 29

= ( 29 x 29) / 2

= 841 / 2

= 420.5 units²

Total area = 841 + 420-5 = 1261.5 units²