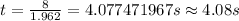Answer:
4.08 s
Step-by-step explanation:
From the law of conservation of momentum, the sum of initial momentum equals the sum of final momentum
Momentum, p=mv where m is the mass and v is the velocity
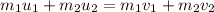 where
where
 and
and
 are the final velocities of the fired projectile and wooden block respectively,
are the final velocities of the fired projectile and wooden block respectively,
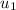 and
and
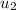 are initial velocities of the fired projectile and wooden block respectively,
are initial velocities of the fired projectile and wooden block respectively,
 and
and
 are masses of the fired projectile and wooden block respectively
are masses of the fired projectile and wooden block respectively
Substituting 200 g=0.2 Kg for
 , 15 Kg for
, 15 Kg for
 , 900 m/s for
, 900 m/s for
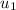 , o m/s for
, o m/s for
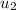 since it's at rest, 300 m/s for
since it's at rest, 300 m/s for
 then
then

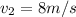
This acts as the initial velocity
Since
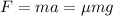
Therefore,

Substituting
 with 0.2 and g with 9.81 then
with 0.2 and g with 9.81 then
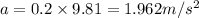
From kinematics equations
v=u-at
since v=0 then
at=u hence
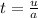
Since we already obtained u as 8 m/s