Question

A human gene carries a certain disease from the mother to the child with a probability rate of 42%.That is, there is a 42% chance that the child becomes infected with the disease. Suppose a femalecarrier of the gene has three children. Assume that the infections of the three children areindependent of one another. Find the probability that at least one of the children get the diseasefrom their mother.A) 0.195B) 0.805C) 0.424D) 0.141

Answer 1

Option B.

Explanation:

It is given that there is a 42% chance that the child becomes infected with the disease.

Let A be the event that the child becomes infected with the disease.

`P(A)=42%=0.42`

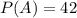
A' be the event that the child is not infected.

`P(A')=1-P(A)=1-0.42=0.58`

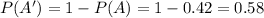
Assume that the infections of the three children are independent of one another.

Let X be the number of children get the disease from their mother.

The probability that all three children are free from disease is

`P(X=0)=P(A')\cdot P(A')\cdot P(A')=0.58\cdot 0.58\cdot 0.58=0.195112`

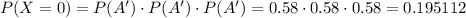
We need to find the probability that at least one of the children get the disease from their mother.

`P(X\ge 1)=1-P(X=0)`

`P(X\ge 1)=1-0.195112`

`P(X\ge 1)=0.804888`

`P(X\ge 1)\approx 0.805`

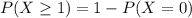
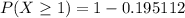
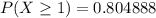
The probability that at least one of the children get the disease from their mother is 0.805.

Therefore, the correct option is B.