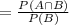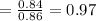Answer:
Explanation:
Let A be the event that Flight departs on time
B be the event that Flight arrive on time
Probability that an airplane flight departs on time
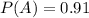
Probability that Flight arrives on time
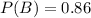
Probability that Flight departs and arrives on time
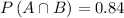
Probability that a flight departed on time given that it arrives on time