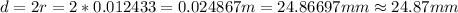Question

Two steel plates are to be held together by means of 16-mm-diameter high-strength steel bolts fitting snugly inside cylindrical brass spacers. Knowing that the average normal stress must not exceed 201 MPa in the bolts and 142 MPa in the spacers, determine the outer diameter of the spacers that yields the most economical and safe design.

Answer 1

24.87 mm

Step-by-step explanation:

The area of the bolt is given by

`A_b=\pi r^(2)`

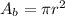
Since diameter is 16mm, the radius is 16/2= 8 mm= 0.008 m

Area,
`A_b=\pi* 0.008^(2)=0.000201062 m^(2)`

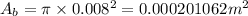
For safe design of the bolt, we use stress of 201 Mpa

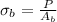`\sigma_b=\frac {P}{A_b}` where P is the load and
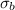`\sigma_b` is normal stress.

Making P the subject then

`P=A_b \sigma_b`

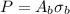
Substituting the figures given and already calculated area of bolt

`P=201* 10^(6)* 0.000201062 m^(2)=40413.4479 N`

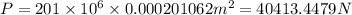
The area of spacer is given by

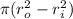`\pi (r_o^(2)- r_i^(2))` where r is radius and the subscripts o and I denote inner and outer respectively

The value of 142 Mpa by default becomes the stress on spacer hence

`\sigma_s=\frac {P}{A_s}` and making
`A_s` the subject then

`A_s=\frac {P}{\sigma_s}`

`\pi (r_o^(2)- r_i^(2))=\frac {P}{\sigma_s}`

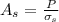
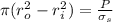
Since we already calculated the value of P as 40413.4479 N and inner radius is 8mm= 0.008 m then

`\pi (r_o^(2)- 0.008^(2))=\frac {40413.4479}{142* 10^(6)}`

`r_o^(2)=0.000154592`

`r=√(0.000154592)=0.012433 m`

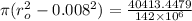
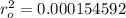
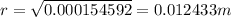
Therefore,
`d=2r=2*0.012433=0.024867 m=24.86697 mm\approx 24.87 mm`