Question

The​ quality-control manager at a compact fluorescent light bulb​ (CFL) factory needs to determine whether the mean life of a large shipment of CFLs is equal to 7463 hours. The population standard deviation is 1080 hours. A random sample of 81 light bulbs indicates a sample mean life of 7163 hours.a. At the 0.05 level of​ significance, is there evidence that the mean life is different from 7 comma 463 hours question markb. Compute the​ p-value and interpret its meaning.c. Construct a 95​% confidence interval estimate of the population mean life of the light bulbs.d. Compare the results of​ (a) and​ (c). What conclusions do you​ reach?a. Let mu be the population mean. Determine the null​hypothesis, Upper H 0​, and the alternative​ hypothesis, Upper H 1.Upper H 0​: Upper H 1​:What is the test​ statistic?Upper Z STAT ​(Round to two decimal places as​ needed.)What​ is/are the critical​ value(s)? ​(Round to two decimal places as needed. Use a comma to separate answers as​ needed.)What is the final​ conclusion?A. Reject Upper H 0. There is sufficient evidence to prove that the mean life is different from 7463 hours.B. Fail to reject Upper H 0. There is sufficient evidence to prove that the mean life is different from 7463 hours.C. Fail to reject Upper H 0. There is not sufficient evidence to prove that the mean life is different from 7463 hours.D. Reject Upper H 0. There is not sufficient evidence to prove that the mean life is different from 7463 hours.b. What is the​ p-value? ​(Round to three decimal places as​needed.)Interpret the meaning of the​ p-value. Choose the correct answer below.A. Fail to reject Upper H 0. There is not sufficient evidence to prove that the mean life is different from 7463 hours.B. Reject Upper H 0. There is sufficient evidence to prove that the mean life is different from 7463 hours.C. Reject Upper H 0. There is not sufficient evidence to prove that the mean life is different from 7463 hours.D. Fail to reject Upper H 0. There is sufficient evidence to prove that the mean life is different from 7463 hours.c. Construct a​ 95% confidence interval estimate of the population mean life of the light bulbs. ​(Round to one decimal place as​ needed.)d. Compare the results of​ (a) and​ (c). What conclusions do you​ reach?A. The results of​ (a) and​ (c) are the​ same: there is not sufficient evidence to prove that the mean life is different from 7463 hours.B. The results of​ (a) and​ (c) are the​ same: there is sufficient evidence to prove that the mean life is different from 7463 hours.C. The results of​ (a) and​ (c) are not the​ same: there is sufficient evidence to prove that the mean life is different from 7463 hours.D. The results of​ (a) and​ (c) are not the​ same: there is not sufficient evidence to prove that the mean life is different from 7463 hours.

Answer 1

Reject the null hypothesis. There is sufficient evidence to prove that the mean life is different from 7463 hours.

95% confidence interval also supports this result.

Explanation:

Let mu be the population mean life of a large shipment of CFLs.

The hypotheses are:

`H_(0)`: mu=7463 hours

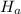`H_(a)`: mu≠7463 hours

Test statistic can be calculated using the equation:

z=
`(X-M)/((s)/(√(N) ) )` where

• X is the sample mean life of CFLs (7163 hours)

• M is the mean life assumed under null hypothesis. (7463 hours)

• s is the population standard deviation (1080 hours)

• N is the sample size (81)

Then z=
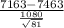`(7163-7463)/((1080)/(√(81) ) )` = -2.5

p-value is 0.0124, critical values at 0.05 significance are ±1.96

At the 0.05 level of​ significance, the the result is significant because 0.0124<0.05. There is significant evidence that mean life of light bulbs is different than 7463 hours.

95% Confidence Interval can be calculated using M±ME where

• M is the sample mean life of a large shipment of CFLs (7163 hours)

• ME is the margin of error from the mean

margin of error (ME) from the mean can be calculated using the formula

ME=
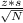`(z*s)/(√(N) )` where

• z is the corresponding statistic in the 95% confidence level (1.96)

• s is the standard deviation of the sample (1080 hours)

• N is the sample size (81)

Then ME=
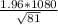`(1.96*1080)/(√(81) )` =235.2

Thus 95% confidence interval estimate of the population mean life of the light bulbs is 7163±235.2 hours. That is between 6927.8 and 7398.2 hours.