Question

A paper describes a study in which researchers observed wait times in coffee shops in Boston. Both wait time and gender of the customer were observed. The mean wait time for a sample of 145 male customers was 85.8 seconds. The mean wait time for a sample of 141 female customers was 113.4 seconds. The sample standard deviations (estimated from graphs that appeared in the paper) were 50 seconds for the sample of males and 75 seconds for the sample of females. For purposes of this exercise, suppose that these two samples are representative of the populations of wait times for female coffee shop customers and for male coffee shop customers. Is there convincing evidence that the mean wait time differs for males and females? Test the relevant hypotheses using a significance level of 0.05. (Use a statistical computer package to calculate the P-value. Use μmales − μfemales. Round your test statistic to two decimal places, your df down to the nearest whole number, and your P-value to three decimal places.)

Answer 1

`t=\frac{85.8-113.4}{\sqrt{((50)^2)/(145)+((75)^2)/(141)}}}=-3.65`

`p_v =2*P(t_((284))<-3.65)=0.000312`

Using Excel we can use the following code: "=2*T.DIST(-3.65;284;TRUE)"

So the p value is a very low value and using any significance level giveen
`\alpha=0.05` always
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and there is enough evidence to conclude that the means are different.

Explanation:

1) Data given and notation

`\bar X_(M)=85.8` represent the mean for the males

`\bar X_(F)=113.4` represent the mean for females

`s_(M)=50` represent the sample standard deviation for males

`s_(F)=75` represent the sample standard deviation for female

`n_(M)=145` sample size for the group poisoned

`n_(F)=141` sample size for the group unpoisoned

t would represent the statistic (variable of interest)

2) Concepts and formulas to use

We need to conduct a hypothesis in order to check if the mean for the two groups are equal or not , the system of hypothesis would be:

Null hypothesis:
`\mu_(M) = \mu_(F)`

Alternative hypothesis:
`\mu_(M) \\eq \mu_(F)`

If we analyze the size for the samples both are higher than 30 but the population deviations are not given, so for this case is better apply a t test to compare means, and the statistic is given by:

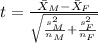`t=\frac{\bar X_(M)-\bar X_(F)}{\sqrt{(s^2_(M))/(n_(M))+(s^2_(F))/(n_(F))}}` (1)

t-test: Is used to compare group means. Is one of the most common tests and is used to determine whether the means of two groups are equal to each other.

3) Calculate the statistic

We can replace in formula (1) the results obtained like this:

`t=\frac{85.8-113.4}{\sqrt{((50)^2)/(145)+((75)^2)/(141)}}}=-3.65`

4) Statistical decision

The first step is calculate the degrees of freedom, on this case:

`df=n_(M)+n_(F)-2=145+141-2=284`

Since is a two tailed test the p value would be:

`p_v =2*P(t_((284))<-3.65)=0.000312`

Using Excel we can use the following code: "=2*T.DIST(-3.65;284;TRUE)"

So the p value is a very low value and using any significance level giveen
`\alpha=0.05` always
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and there is enough evidence to conclude that the means are different.