Question

Consider a large square plate with sides length L = 1 meter moving on a thin film of oil of thickness h, L≫ℎ ( h=0.0001meters). If the plate is moved with velocity U = 0.1 m/s, and the viscosity of the oil is μ= 0.968/kgm.s(i.e., SAE 30), and you ignore any edge effects. What is the viscous shear stress τyx and drag force (D= τyx. Area )?

Answer 1

The viscous shear stress is 968 Pa (or can be written as 968
`N/m^2`) and the drag force is 968 N.

Step-by-step explanation:

Viscous shear stress

For a parallel flow of a Newtonian fluid, the shear stress is proportional to the gradient of the velocity,

`\tau_(yx)= \mu \cfrac{du}{dy}`

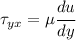
Considering a large square plate moving on a thin film of thickness h, the velocity profile is

`u(y) = U\cfrac{y}{h}`

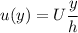
Thus its derivative will be just

`\cfrac{du}{dy}= \cfrac U h`

So replacing on the viscous shear stress formula we get

`\tau_(yx)= \mu \cfrac {U}h`

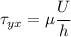
We can then replace the given information

`\tau_(yx)= 0.968 * \cfrac{kg}{m*  s}* \cfrac{0.1 \cfrac ms}{0.0001 \, m}`

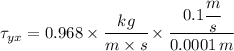
Evaluating we get

`\boxed{\tau_(yx)=968\, Pa}`

The viscous shear stress is 968 Pascals or
`N/m^2`.

Drag force

Using the given equation for the drag force we have

`D = \tau_(yx) A`

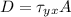
And since we have a large square plate of sides L we can write the area as

`A = L^2`

So the drag force is

`D = \tau_(yx) L^2`

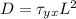
Replacing values

`D = 968\, Pa * (1\, m)^2`

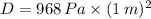
We get

`\boxed{D= 968 \,N}`

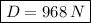
The drag force is 968 N.