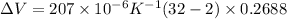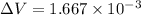Question

An ordinary drinking glass is filled to the brim with water (268.4 mL) at 2.0 ° C and placed on the sunny pool deck for a swimmer to enjoy. If the temperature of the water rises to 32.0 ° C before the swimmer reaches for the glass, how much water will have spilled over the top of the glass? Assume the glass does not expand.

Answer 1

`\Delta V=1.667*10^(-3)`

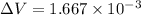
Step-by-step explanation:

Given the initial temperature T_i=2° C

final temperature T_f= 32° C

The original volume of water Vo=268.8 mL= 0.2688 L

we need to calculate the change in the volume

As we know that volume expansion is given by

`(\Delta V)/(V_0)= \beta\Delta T`

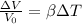
ΔV= change in Volume

β= expansion coefficient =
`207*10^(-6) K^(-1)`

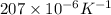
therefore,

`\Delta V= \beta\Delta T V_0`

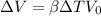
plugging values we get

`\Delta V=207*10^(-6) K^(-1) (32-2)*0.2688`

`\Delta V=1.667*10^(-3)`