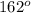Question

If three of the interior angles of a convex hexagon each measure 140, a fourth angle measures 84, and the

measure of the fifth angle is 3 times the measure of the sixth angle, find the measure of the sixth angle.

Answer 1

54

Explanation:

Answer 2

The sixth angle of the hexagon is
`54^(o)`.

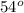Explanation:

A convex hexagon is one that does not have equal length of sides i.e it is irregular.

Sum of angles in a polygon = (n - 2) x 180

For an hexagon, n = 6.

Sum of angles in a hexagon = (6 - 2) x 180

= 4 x 180

=
`720^(o)`

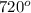
Therefore, let the sixth angle be represented by x, so that;

`140^(o)` +
`140^(o)` +
`140^(o)` +
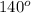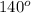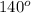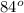`84^(o)` + 3x + x =
`720^(o)`

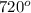
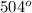`504^(o)` + 4x =
`720^(o)`

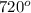
4x =
`720^(o)` -
`504^(o)`

=
`216^(o)`

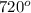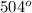
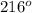
x =
`(216)/(4)`

=
`54^(o)`

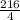
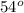
The sixth angle of the hexagon is
`54^(o)`.

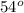Fifth angle = 3 x
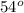
`54^(o)`

=
`162^(o)`