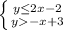Question

In the graph below, the area above f(x) is shaded and labeled A, the area below g(x) is shaded and labeled B, and the area where f(x) and g(x) have shading in common is labeled AB.

The graph below represents which system of inequalities?

(A) y > 2x − 3
y > −x − 3
(B) y < 2x − 2
y < −x + 3
(C) y ≤ 2x − 2
y > −x + 3
(D) None of the above

Answer 1

Answer: OPTION C.

Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Notice that the line of f(x) is dashed. This means that the symbol of the inequality must be
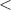`<` or
`>`.

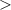Since the shaded region A is above the line, the symbol is
`>`

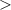
Observe that its y-intercept is:

`b=3`

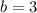
The line of g(x) is solid. This means that the symbol of the inequality must be
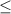`\leq` or
`\geq`.

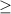Since the shaded region B is below the line, the symbol is
`\leq` .

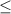Observe that its y-intercept is:

`b=-2`.

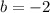Based on this, we can conclude that the graph represents the following System of Inequalities:

`\left \{ {{y\leq 2x -2} \atop {y >-x + 3}} \right.`