Question

Three people get into an empty elevator at the first floor of a building that has 10 floors. Each presses the button for their desired floor (unless one of the others has already pressed that button). Assume that they are equally likely to want to go to floors 2 through 10 (independently of each other). What is the probability that the buttons for 3 consecutive floors are pressed?

Answer 1

The probability that the buttons for 3 consecutive floors are pressed is approximately 4.9%.

Step-by-step explanation:

To find the probability that the buttons for 3 consecutive floors are pressed, we need to consider the different scenarios in which this can happen. Let's assign the three people as Person A, Person B, and Person C. Person A can press any button from floor 2 to floor 8 (as they cannot press the button for the first floor). Person B can then press the button for the floor either one above or one below the floor that Person A pressed. Finally, Person C can press the button either one above or one below the floor that Person B pressed. Since there are 7 possible floors for Person A, 2 possible floors for Person B, and 2 possible floors for Person C, the total number of ways that the buttons for 3 consecutive floors can be pressed is 7 * 2 * 2 = 28.

Now, let's find the total number of possible combinations of floors that the three people can press. Person A has 7 possible floors to choose from (excluding floor 1), Person B has 9 possible floors to choose from (including the floor that Person A pressed), and Person C has 9 possible floors to choose from (including the floor that Person B pressed). Therefore, the total number of possible combinations is 7 * 9 * 9 = 567.

Finally, to find the probability that the buttons for 3 consecutive floors are pressed, we divide the number of ways that the buttons can be pressed by the total number of possible combinations. So the probability is 28 / 567 ≈ 0.0494, or about 4.9%.

Answer 2

The probability that the buttons for 3 consecutive floors are pressed is
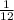`(1)/(12)` or 0.0833

Step-by-step explanation:

Consider the provided information.

They are equally likely to want to go to floors 2 through 10.

That means the number of buttons are 9.

Each presses the button for their desired floor (unless one of the others has already pressed that button).

It means that if two people wants to go at the same floors, then only one person will press the button.

Therefore, the total number of ways are: 9×8×7=504

Three consecutive floors means they have been picked:

2,3,4 or 3,4,5 or 4,5,6 or 5,6,7 or 6,7,8 or 7,8,9 or 8,9,10

We have 3 persons that means we can arrange them in 3! ways.

Therefore, the total number of favorable outcomes for this case is 7×3!=42

`Probability = \frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}}`

`Probability = (42)/(504)=(1)/(12)`

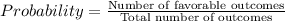
Hence, the probability that the buttons for 3 consecutive floors are pressed is
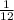`(1)/(12)` or 0.0833