Answer:
Option A) About ±2.98 minutes
Explanation:
We are given the following information in the question:
Sample mean,
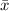 = 191.3 minutes
= 191.3 minutes
Sample size, n = 200
Population standard deviation, σ = 21.5 minutes
Alpha, α = 0.05
The leaders of the organization wish to develop an interval estimate with 95 percent confidence.
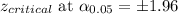
Margin of error =
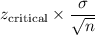
Putting the values, we get:
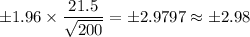
Option A) About ±2.98 minutes