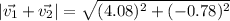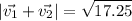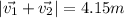Question

Find the magnitude of the sum

of these two vectors::
14m
30.0°
60.00
magnitude (m)

Answer 1

`\displaystyle |\vec{v_1}+\vec{v_2}|=4.15m`

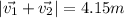
Step-by-step explanation:

Sum of Vectors in the Plane

Given two vectors

`\displaystyle \vec{v_1}\ ,\ \vec{v_2}`

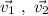
They can be expressed in their rectangular components as

`\displaystyle \vec{v_1}=<x_1\ ,\ y_1>`

`\displaystyle \vec{v_2}=<x_2\ ,\ y_2>`

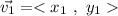
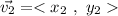
The sum of both vectors can be done by adding individually its components

`\displaystyle \vec{v_1}+\vec{v_2}=<x_1+x_2\ ,\ y_1+y_2>`

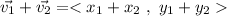
If the vectors are given as a magnitude and an angle
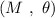`(M\ ,\ \theta )`, each component can be found as

`\displaystyle \vec{v_1}=<M_1 cos\theta_1\ ,\ M_1sin\theta _1>`

`\displaystyle \vec{v_2}=<M_2 cos\theta_2\ ,\ M_2sin\theta_2>`

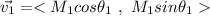
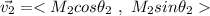
The first vector has a magnitude of 3.14 m and an angle of 30°, so

`\displaystyle \vec{v_1}=<3.14\ cos30^o,3.14\ sin30^o>`

`\displaystyle \vec{v_1}=<2.72,1.57>`

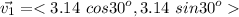
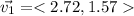
The second vector has a magnitude of 2.71 m and an angle of -60°, so

`\displaystyle \vec{v_2}=<2.71cos(-60^o),2.71sin(-60^o)>`

`\displaystyle \vec{v_2}=<1.36,-2.35>`

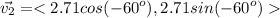
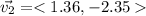
The sum of the vectors is

`\displaystyle \vec{v_1}+\vec{v_2}=<2.72+1.36,1.57-2.35>`

`\displaystyle \vec{v_1}-\vec{v_2}=<4.08,-0.78>`

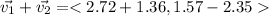
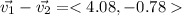
Finally, we compute the magnitude of the sum

`\displaystyle |\vec{v_1}+\vec{v_2}|=√((4.08)^2+(-0.78)^2)`

`\displaystyle |\vec{v_1}+\vec{v_2}|=√(17.25)`

`\displaystyle |\vec{v_1}+\vec{v_2}|=4.15m`